Code examples¶
Dry mass computation with radial inclusion factor¶
This examples illustrates the usage of the “radial inclusion factor”
which is defined in the configuration section “sphere” and used in
drymass.anasphere.relative_dry_mass() with the
keyword argument rad_fact.
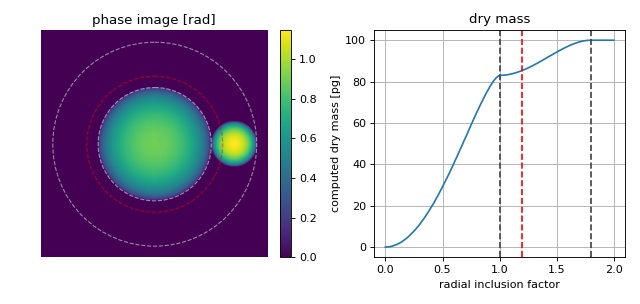
The phase image is computed from two spheres whose dry masses add up to 100pg with the larger sphere having a dry mass of 83pg. The larger sphere is located at the center of the image which is also used as the origin for dry mass computation. The radius of the larger sphere is known (10µm). Thus, the corresponding radius (inner circle) corresponds to a radial inclusion factor of 1. In DryMass, the default radial inclusion factor is set to 1.2 (red). In some cases, this inclusion factor must be increased or decreased depending on whether additional information (the smaller sphere) should be included in the dry mass computation or not.
mass_radial_inclusion_factor.py
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 | from drymass.anasphere import relative_dry_mass
import matplotlib
import matplotlib.pylab as plt
import numpy as np
import qpimage
import qpsphere
# refraction increment
alpha = .18 # [mL/g]
# general simulation parameters
medium_index = 1.333
model = "projection"
wavelength = 500e-9 # [m]
pixel_size = 1e-7 # [m]
grid_size = (400, 400) # [px]
# sphere parameters
dry_masses = [83, 17] # [pg]
radii = [10, 4] # [µm]
centers = [(200, 200), (200, 340)] # [px]
phase_data = np.zeros(grid_size, dtype=float)
for m, r, c in zip(dry_masses, radii, centers):
# compute refractive index from dry mass
r_m = r * 1e-6
alpha_m3g = alpha * 1e-6
m_g = m * 1e-12
n = 1.333 + 3 * alpha_m3g * m_g / (4 * np.pi * (r_m**3))
# generate example dataset
qpi = qpsphere.simulate(radius=r_m,
sphere_index=n,
medium_index=medium_index,
wavelength=wavelength,
pixel_size=pixel_size,
model=model,
grid_size=grid_size,
center=c)
phase_data += qpi.pha
qpi_sum = qpimage.QPImage(data=phase_data,
which_data="phase",
meta_data={"wavelength": wavelength,
"pixel size": pixel_size,
"medium index": medium_index})
# compute dry mass in dependence of radius
mass_evolution = []
mass_radii = []
for rad_fact in np.linspace(0, 2.0, 100):
dm = relative_dry_mass(qpi=qpi_sum,
radius=radii[0] * 1e-6,
center=centers[0],
alpha=alpha,
rad_fact=rad_fact)
mass_evolution.append(dm * 1e12)
mass_radii.append(rad_fact)
# plot results
fig = plt.figure(figsize=(8, 3.8))
matplotlib.rcParams["image.interpolation"] = "bicubic"
# phase image
ax1 = plt.subplot(121, title="phase image [rad]")
ax1.axis("off")
map1 = ax1.imshow(qpi_sum.pha)
plt.colorbar(map1, ax=ax1, fraction=.048, pad=0.05)
# dry mass vs. inclusion factor
ax2 = plt.subplot(122, title="dry mass")
ax2.plot(mass_radii, mass_evolution)
ax2.set_ylabel("computed dry mass [pg]")
ax2.set_xlabel("radial inclusion factor")
ax2.grid()
# radius indicators
for r in [100, 180]:
cx = centers[0][0] + .5
cy = centers[0][1] + .5
circle = plt.Circle((cx, cy), r,
color='w', fill=False, ls="dashed", lw=1, alpha=.5)
ax1.add_artist(circle)
ax2.axvline(r / 100, color="#404040", ls="dashed")
# add default
circle = plt.Circle((cx, cy), 120,
color='r', fill=False, ls="dashed", lw=1, alpha=.5)
ax1.add_artist(circle)
ax2.axvline(1.2, color="r", ls="dashed")
plt.tight_layout()
plt.show()
|
Comparison of relative and absolute dry mass¶
Relative dry mass is the dry mass computed relative to the surrounding medium. If the refractive index of the surrounding medium does not match that of the intracellular fluid (approximately 1.335), then the relative dry mass underestimates the actual dry mass. For a spherical cell, the absolute (corrected) dry mass can be computed as described in the theory section on dry mass computation.
This examples compares the relative dry mass
(drymass.ansphere.relative_dry_mass()) to the
absolute dry mass corrected for a spherical phase object
(drymass.ansphere.absolute_dry_mass_sphere()).
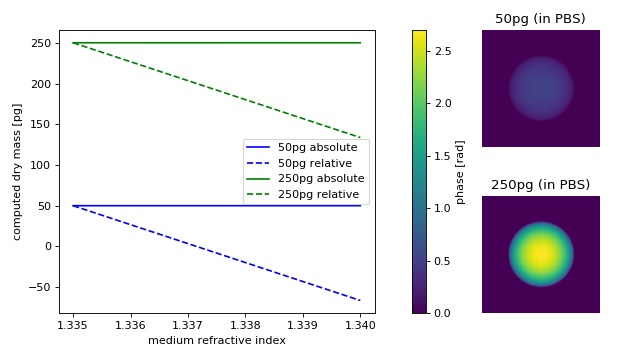
From simulated phase images (projection approach, wavelength 550nm)
of two cell-like spheres with a radius of 10µm and dry masses of
50pg (n≈1.337) and 250pg (n≈1.346), the absolute and relative dry
masses are computed with varying refractive index of the medium.
At the refractive index of phosphate buffered saline (PBS), absolute and relative dry mass are equivalent. As the refractive index of the medium increases, the relative drymass decreases linearly (independent of dry mass), underestimating the actual dry mass.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 | from drymass.anasphere import absolute_dry_mass_sphere, relative_dry_mass
import matplotlib
import matplotlib.pylab as plt
import numpy as np
import qpsphere
# refraction increment
alpha = .18 # [mL/g]
# general simulation parameters
model = "projection"
wavelength = 500e-9 # [m]
pixel_size = 1.8e-7 # [m]
grid_size = (200, 200) # [px]
# sphere parameters
radius = 10 # [µm]
center = (100, 100) # [px]
dry_masses = [50, 250] # [pg]
medium_indices = np.linspace(1.335, 1.34, 5)
qpi_pbs = {}
m_abs = {}
m_rel = {}
phase_data = np.zeros(grid_size, dtype=float)
for m in dry_masses:
# initiate results list
m_abs[m] = []
m_rel[m] = []
# compute refractive index from dry mass
r_m = radius * 1e-6
alpha_m3g = alpha * 1e-6
m_g = m * 1e-12
n = 1.335 + 3 * alpha_m3g * m_g / (4 * np.pi * (r_m**3))
for medium_index in medium_indices:
# generate example dataset
qpi = qpsphere.simulate(radius=r_m,
sphere_index=n,
medium_index=medium_index,
wavelength=wavelength,
pixel_size=pixel_size,
model=model,
grid_size=grid_size,
center=center)
# absolute dry mass
ma = absolute_dry_mass_sphere(qpi=qpi,
radius=r_m,
center=center,
alpha=alpha,
rad_fact=1.2)
m_abs[m].append(ma * 1e12)
# relative dry mass
mr = relative_dry_mass(qpi=qpi,
radius=r_m,
center=center,
alpha=alpha,
rad_fact=1.2)
m_rel[m].append(mr * 1e12)
if medium_index == 1.335:
qpi_pbs[m] = qpi
# plot results
fig = plt.figure(figsize=(8, 4.5))
matplotlib.rcParams["image.interpolation"] = "bicubic"
# phase images
kw = {"vmax": qpi_pbs[dry_masses[1]].pha.max(),
"vmin": qpi_pbs[dry_masses[1]].pha.min()}
ax1 = plt.subplot2grid((2, 3), (0, 2))
ax1.set_title("{}pg (in PBS)".format(dry_masses[0]))
ax1.axis("off")
map1 = ax1.imshow(qpi_pbs[dry_masses[0]].pha, **kw)
ax2 = plt.subplot2grid((2, 3), (1, 2))
ax2.set_title("{}pg (in PBS)".format(dry_masses[1]))
ax2.axis("off")
ax2.imshow(qpi_pbs[dry_masses[1]].pha, **kw)
# overview plot
ax3 = plt.subplot2grid((2, 3), (0, 0), colspan=2, rowspan=2)
ax3.set_xlabel("medium refractive index")
ax3.set_ylabel("computed dry mass [pg]")
for m, c in zip(dry_masses, ["blue", "green"]):
ax3.plot(medium_indices, m_abs[m], ls="solid", color=c,
label="{}pg absolute".format(m))
ax3.plot(medium_indices, m_rel[m], ls="dashed", color=c,
label="{}pg relative".format(m))
ax3.legend()
plt.colorbar(map1, ax=ax3, fraction=.048, pad=0.1,
label="phase [rad]")
plt.tight_layout()
plt.subplots_adjust(wspace=.14)
plt.show()
|